Em jogos digitais é natural utilizar o sistema cartesiano para localização de objetos por meio de pontos. Dessa forma, pode-se criar métodos para:

• Descobrir a distância de um objeto ao outro;
• Encontrar um NPC, mais próximo;
• Calcular distância para verificar um possível ataque do NPC.

O que você sabe sobre ?

O plano cartesiano pode ser plano ou espacial. Para melhor compreensão vamos aprender primeiro sobre o sistema plano.

O sistema plano é composto pela intersecção de dois segmentos de retas orientadas perpendiculares. A reta horizontal é conhecida como eixo das abcissas (x) e sua companheira eixo das ordenadas (y). 

Na computação, usamos a expressão 2D ou 3D, e é isso que nos interessa e muito. A Figura 1 apresenta o nosso lindo plano cartesiano, com seus quadrantes e seus pontos. Para nosso exemplo estamos considerando apenas o 2D, certo? 

Figura 1 – Plano cartesiano

 

Observa que cada quadrante possui uma configuração específica. Por exemplo,  o ponto P(3,-2) pertence ao quarto quadrante. Isso significa que podemos prever a posição de cada ponto somente observando os sinais. 

Agora, vamos para o próximo passo, que é o cálculo da distância e sua direção. O cálculo da distância é algo muito comum em jogos digitais. Com ela, você pode fazer várias aplicações dentro do jogo como:

• Descobrir a distância de um objeto ao outro;
• Encontrar um NPC, mais próximo;
• Calcular distância para verificar um possível ataque do NPC.

Para calcular a distância você precisa conhecer os pontos dos objetos dentro do plano, e calcular a variação, tanto dos pontos das abscissas e ordenadas.  Veja a Figura 2 com dois pontos dentro do jogo.

Figura 2 – Localização dos pontos no sistema

Nesse sentido, podemos observar na Figura 2 um triângulo retângulo, então vamos aplicar o teorema de Pitágoras para calcularmos a distância.  🙂 

D = SQRT((xa-xb)2+(ya-yb)2)

Observação: SQRT é a raiz Quadrada

Importante destacar: deve-se calcular a posição do alvo – posição de origem.

Problematização

Desejo criar um jogo onde os NPCs devem localizar o Player e segui-lo!    

Vamos colocar dois personagens, o Player e o NPC, como mostra a Figura 3.  

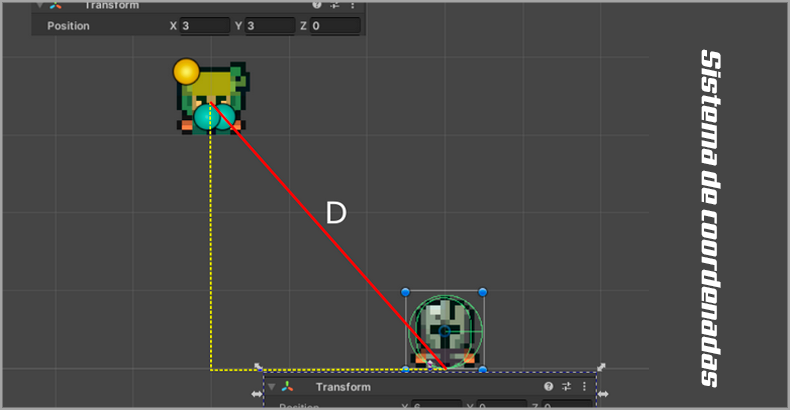
Figura 3 – Personagens posicionados dentro do sistema da Unity

Nosso Player está na posição P1(3,3) e o NPC em P2(6,3). Note então que os dois personagens estão no quadrante 1.   

Pare e reflita: O plano cartesiano é muito importante em jogos digitais?

Vamos codificar isso na Unity? 

void Update()
{
// Direcao = destino – origem = (x2-x1), (y2-y1)
Vector3 direcao = player.position – transform.position;
Debug.Log(“A direção entre o player e o inimigo” + direcao);
Debug.DrawRay(transform.position, direcao, Color.cyan);

Debug.Log(“A magnitude” + direcao.magnitude);

transform.Translate(direcao * Time.deltaTime * 2f);

}

A seguir será comentado todas as linhas para melhor compreensão

Para calcular a distância entre os dois personagens, precisamos conhecer a posição do player. Para isso, criamos uma variável do tipo Transform com o nome de player.

[SerializeField] private Transform player;

No método Update, deve-se calcular a variação das coordenadas no eixo X e Y dos personagens.

Vector3 direcao = player.position – transform.position;

No que resulta: Px(3-6), Py(3-0) = P(-6,3)

Com a classe Debug e o método Log podemos verificar o resultado.

Debug.Log(“A direção entre o player e o inimigo” + direcao);

Para verificar a distância podemos traçar uma linha na tela com a classe Debug e o método DrawRay. 

Debug.DrawRay(transform.position, direcao, Color.cyan);

Finalmente, podemos verificar a distância com a propriedade Magnitude

Debug.Log(“A magnitude” + direcao.magnitude);

Agora podemos brincar de seguir o player com a linha a seguir:

transform.Translate(direcao * Time.deltaTime * 2f);

Caso deseje visualizar esse conteúdo em vídeo: