Perceptron de Uma Camada: A Vovozinha das Redes Neurais
Em 1958 Frank Rosenblatt deu vida a perceptron de uma camada, também conhecida como perceptron simples, a vovozinha das redes neurais, sendo o modelo mais simplista de uma rede neural, não podemos esperar que ela faça malabarismos, mas ainda assim, tem seu charme. Este modelo funciona como um classificador linear, mas o que é um classificador linear? Imagine que você está criando um jogo, onde cada soldado precisa tomar decisões com base em informações que recebe, e assim deve decidir se deve atacar ou não. Pois é, parece um “if e else” sofistificado e cheio de operações matemáticas. Nesse contexto, as entradas definem a saída. Essas entradas são propriedades que definem o comportamento do soldado, como a distância euclidiana, quantidade de munições, entre outros atributos. Porém, “Perceptronauta”, para começar de maneira simples, irei introduzir um perceptron usando as portas AND e XOR, e descobrir uns segredinhos. É como ensinar a vovó a distinguir entre chá e café: básico, mas essencial para construir conhecimentos mais complexos! Vamos nessa então!
Estrutura do Perceptron
A estrutura de uma rede neural é simples, mas os processos por trás dela são como um quebra-cabeça. Os neurônios são as unidades básicas que processam informações. Eles são inspirados nos neurônios biológicos, e têm a seguinte estrutura básica, veja a Figura 1.0 e a descrição a seguir:
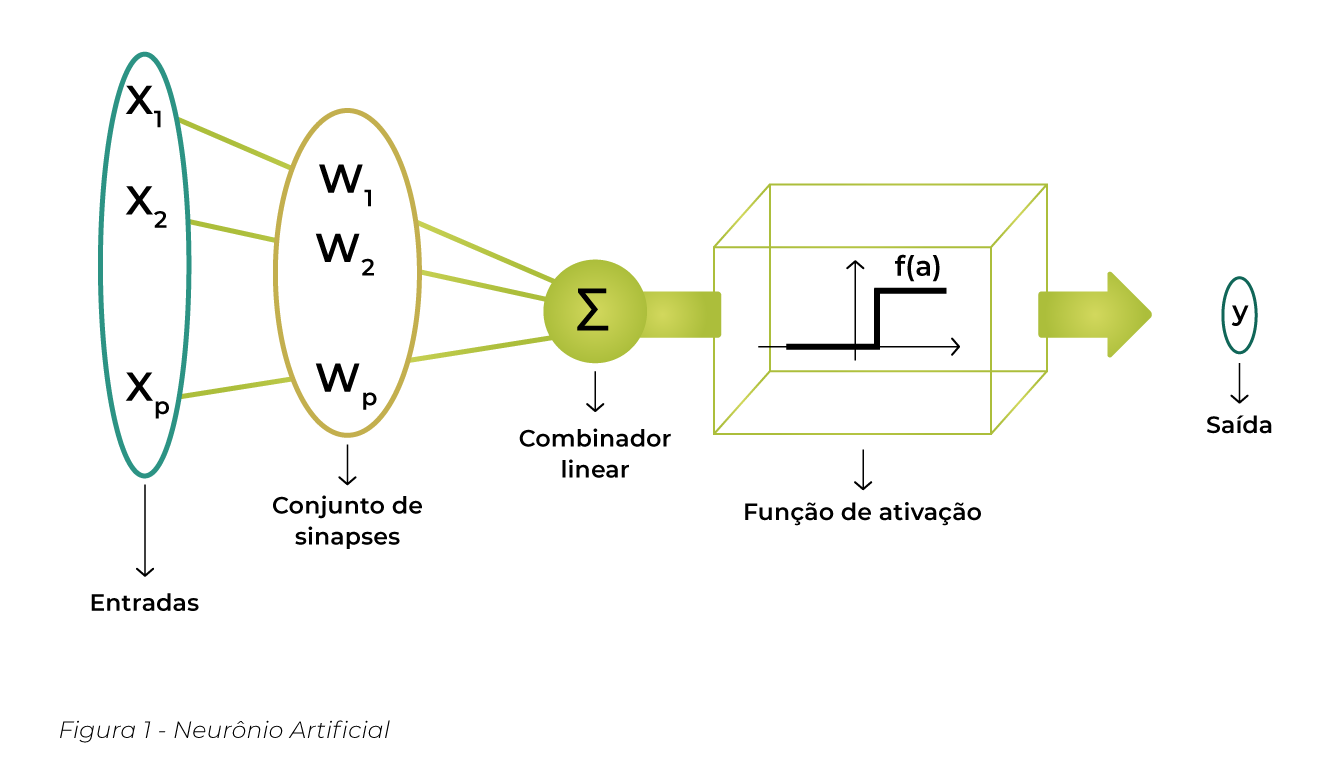
Figura 1.0 – Redes Neurais
- Entradas (Inputs): Neurônios recebem múltiplas entradas, cada uma com um peso;
- Pesos (Weights): Ajustam a força de cada entrada para minimizar erros. Anote num caderninho essa informação;
- Função de Soma (Summation Function): Calcula a soma ponderada das entradas;
- Função de Ativação (Activation Function): Após calcular a soma ponderada, o neurônio aplica uma função de ativação.
Batalha das Separabilidades: Lineares vs. Não Lineares
Lembra do segredinho que te falei no começo deste post? Os problemas podem ser linearmente separáveis ou não linearmente separáveis:
- Linearmente Separáveis: Esses são os problemas linearmente separáveis! Uma única linha reta é tudo o que precisamos para dividir as classes. Um exemplo clássico é a Porta AND, onde tudo se encaixa direitinho com uma linha reta bem no meio.
- Não Linearmente Separáveis: Agora, as coisas ficam mais caóticas com os problemas não linearmente separáveis. Aqui, uma única linha reta não resolve a bagunça. Pense na Porta XOR, onde uma simples linha reta falha miseravelmente. Para vencer essa batalha, precisamos de armas mais sofisticadas: redes neurais mais complexas! As MLPs (Multi-Layer Perceptrons) entram em cena, capazes de capturar todas as nuances e relações não lineares nos dados, garantindo a vitória no campo de batalha da separabilidade.
Operadores Lógicos: Os Super-Herois da Computação
Imagine um mundo onde pequenos herois trabalham incansavelmente para tomar decisões e resolver problemas. Esses herois são os operadores lógicos, cada um com suas habilidades especiais para determinar resultados baseados em condições específicas. Vamos conhecer dois desses super-herois da computação para o nosso estudo de caso.
A Super And
Imagine que você está jogando um jogo de aventura. Para abrir o Baú Mágica do tesouro, você precisa de duas chaves especiais: a Chave de Ouro e a Chave de Prata. Só quando você tem ambas as chaves, a porta se abre. Vamos ver isso na prática com a tabela verdade da porta AND:
| Chave de Ouro (Entrada 1) | Chave de Prata (Entrada 2) | Baú (Saída) | |
| 0 | 0 | 0 | (0,0 ) O baú do tesouro não abre. |
| 0 | 1 | 0 | (0,1 ) O baú permanece fechado |
| 1 | 0 | 0 | (1,0 ) O baú permanece fechado |
| 1 | 1 | 1 | (1,1) O baú se abre e você encontra o tesouro! |
Lembra-se que eu te contei? As entradas (chaves de ouro e chave de prata) são as propriedades da rede, lembra? e a saída o que queremos. Veja o gráfico da Figura 2.0, o que você vê?
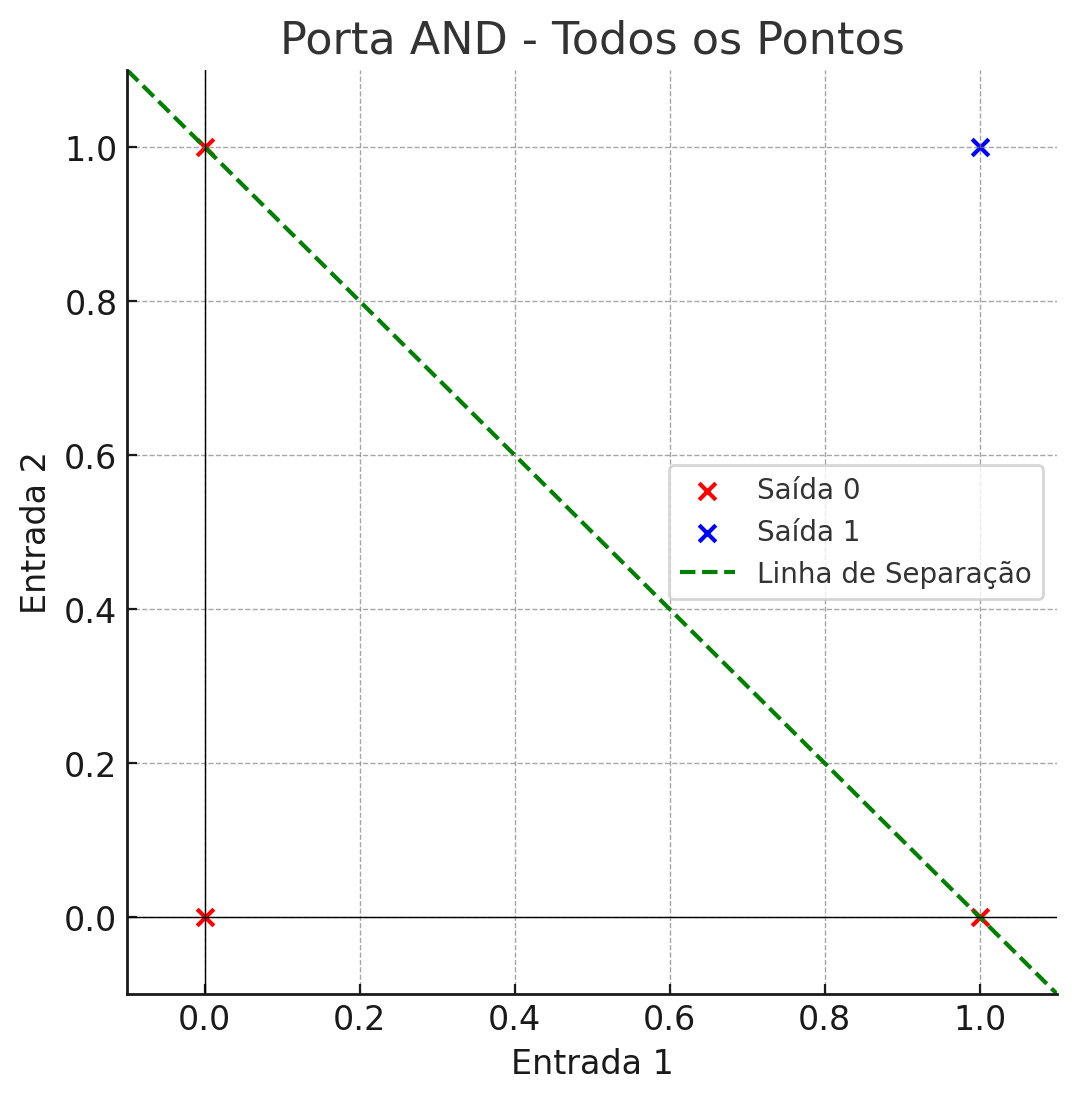
Figura 2.0 – Operador And
Veja que temos os dados linearmente separáveis, isso significa que a perceptron simples pode aprender a classificação correta e convergir para as saídas desejadas.
- Os pontos vermelhos representam as entradas com saída 0;
- Os pontos azuis representam as entradas com saída 1;
- A linha verde tracejada representa a linha de separação linear.
A Super XOR
| Chave de Ouro (Entrada 1) | Chave de Prata (Entrada 2) | Baú (Saída) | |
| 0 | 0 | 0 | (0,0 ) O baú do tesouro não abre. |
| 0 | 1 | 1 | (0,1 ) O baú abre |
| 1 | 0 | 1 | (1,0 ) O baú abre |
| 1 | 1 | 0 | (1,1) O baú do tesouro não abre. |
A porta XOR não é linearmente separável. Não existe uma linha reta que possa separar as saídas 0 das saídas 1 no plano de entrada. Veja a Figura 3.0:
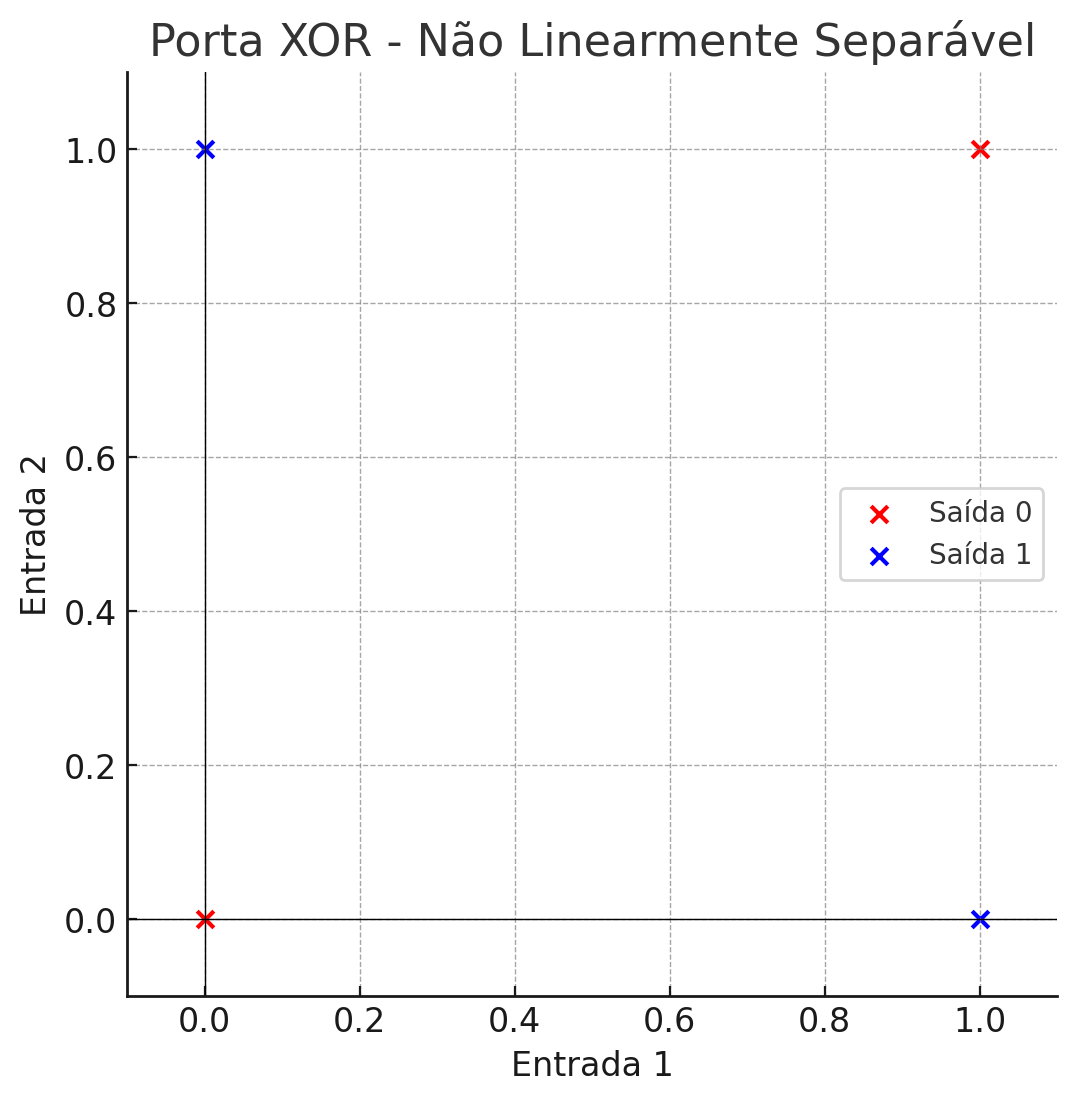
Figura 3.0 – Operador Xor
Você consegue traçar uma linha reta para separar?
- Os pontos vermelhos representam as entradas com saída 0.
- Os pontos azuis representam as entradas com saída 1.
Como podemos ver, não é possível desenhar uma única linha reta que separa os pontos das duas classes (saídas 0 e 1). Portanto, a porta XOR não é linearmente separável para a perceptron de uma camada.
O Cérebro do Perceptron: Decodificando os Cálculos e Ajustes
1. Previsão (Predict)
Para prever a saída, o perceptron calcula uma soma ponderada das entradas multiplicadas pelos pesos correspondentes e, em seguida, aplica a função de ativação.
Soma Ponderada:
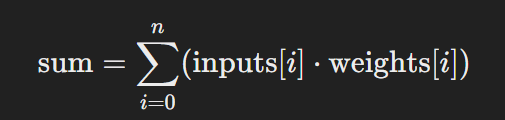
Função de Ativação (Step Function):

Ajuste dos Pesos (Train)
Durante o treinamento, o perceptron ajusta os pesos para minimizar o erro entre a previsão e o rótulo (label) desejado.
Erro: Indica a discrepância entre a previsão do perceptron e o valor da saída (desejada). Esse erro é utilizado para ajustar os pesos do perceptron, de modo que futuras previsões sejam mais precisas.
![]()
Ajuste dos Pesos
![]()
Configurações Iniciais
Pesos Inicializados: weights=[0.2, -0.1]
- Descrição: Valores atribuídos a cada entrada do perceptron que determinam a influência dessas entradas na saída final. Inicializar os pesos significa atribuir valores iniciais a eles antes do início do treinamento.
- Importância: Escolher pesos iniciais aleatórios pequenos ajuda a quebrar a simetria e a permitir que o modelo aprenda adequadamente durante o treinamento.
Taxa de Aprendizado
Taxa de Aprendizado: learningRate=0.01
- Descrição: Hiperparâmetro que controla a quantidade de ajuste nos pesos em cada iteração do treinamento.
- Importância: Um valor de 0.01 ajusta os pesos lentamente, garantindo que o modelo converja de forma estável. Valores muito altos podem impedir a convergência, enquanto valores muito baixos tornam o treinamento lento.
Dados de Treinamento
Dados de Treinamento: trainingInputs = [{0,0}, {0,1}, {1,0}, {1,1}]
- Descrição: Conjuntos de entradas usadas pelo perceptron para aprender. Cada par {x1, x2} representa uma combinação de valores de entrada para treinar o modelo.
- Importância: Fornecem exemplos a partir dos quais o perceptron aprenderá a classificar ou prever a saída correta. Exemplos simples ajudam a demonstrar a lógica do perceptron.
Labels
Labels: labels= [0, 0, 0, 1]
- Descrição: Valores esperados de saída para cada conjunto de entradas nos dados de treinamento. Representam a “verdade” que o perceptron deve aprender a prever.
- Importância: Usados para calcular o erro durante o treinamento. O perceptron ajusta seus pesos para minimizar a diferença entre suas previsões e esses valores de saída esperados.
Época
Época: 10
- Descrição: Um ciclo completo através de todo o conjunto de dados de treinamento. O número de épocas especifica quantas vezes o modelo passará por todo o conjunto de dados durante o treinamento.
- Importância: Treinar o modelo por múltiplas épocas permite ajustes repetidos dos pesos, melhorando a precisão. Mais épocas geralmente resultam em um modelo mais bem treinado, mas excesso pode causar overfitting.
| Época | Iteração | Entradas | Pesos Iniciais | Soma Ponderada | Previsão | Erro | Ajuste dos Pesos | Novos Pesos |
| 1 | 1 | (0,0) | [0.2, -0.1] | 0*0.2 + 0* (-0.1) | 1 | -1 | [0.2 + (-1)*0*0.01, -0.1 + (-1)*0*0.01] | [0.2, -0.1] |
| 1 | 2 | (0,1) | [0.2, -0.1] | 0*0.2 + 0* (-0.1) | 0 | 0 | [0.2 + 0*0*0.01, -0.1 + 0*1*0.01] | [0.2, -0.1] |
| 1 | 3 | (1, 0) | [0.2, -0.1] | 0.2*1 + (-0.1)*0 = 0.2 | 1 | -1 | [0.2 + (-1)*1*0.01, -0.1 + (-1)*0*0.01] | [0.19, -0.1] |
| 1 | 4 | (1, 1) | [0.19, -0.1] | 0.19*1 + (-0.1)*1 = 0.09 | 1 | 0 | [0.19 + 0*1*0.01, -0.1 + 0*1*0.01] | [0.19, -0.1] |
Você irá fazer essa iteração até que todos os erros fiquem igual a zero. Entretanto note, que a próxima rodada a época será 2, e consequentemente os pesos iniciais serão substituídos pelos novos pesos.
Conclusão
Distinguir entre problemas linearmente separáveis e não separáveis ajuda a escolher o modelo adequado para o problemas. Problemas complexos e realistas, como o de abrir o Baú Mágico do Tesouro com a lógica XOR, geralmente exigem modelos não lineares mais avançados para alcançar uma performance aceitável. No caso da porta XOR, a complexidade adicional requer um modelo mais sofisticado, como uma rede neural de múltiplas camadas, para resolver o problema de forma eficaz.
